ในการศึกษาตรีโกณมิติอาศัยความรู้เรื่องของสามเหลี่ยมคล้าย ซึ่งจะนำมาใช้ประโยชน์ในการหาความยาวด้านทั้งสามด้านของรูปสามเหลี่ยมที่เป็นรูปสามเหลี่ยมมุมฉากโดยใช้หลักการว่า “อัตราส่วนของความยามของด้านที่อยู่ตรงข้ามมุมที่เท่ากันจะเท่ากัน”

1. อธิบายความสัมพันธ์ของรูปสามเหลี่ยมคล้ายกับตรีโกณมิติ
2. เขียนแสดงเกี่ยวกับความสัมพันธ์ของรูปสามเหลี่ยมคล้ายกับตรีโกณมิติ
3. มีความคิดรวบยอดเกี่ยวกับตรีโกณมิติและนำหลักการไปเชื่อมโยงใช้ในชีวิตประจำวันได้
4. มีเจตคติที่ดีต่อวิชาคณิตศาสตร์

พิจารณารูปสามเหลี่ยมต่อไปนี้

                ตรีโกณมิติมาจากภาษาอังกฤษว่า trigonometry หมายถึง “วัดรูปสามเหลี่ยม” โดยที่  “tri” หมายถึง three ซึ่งแปลว่า สาม “gon” หมายถึง “angle” ซึ่งแปลว่า มุม และ “metry” หมายถึง measure ซึ่งแปลว่า วัด

                การศึกษาตรีโกณมิติอาศัยความรู้ในเรื่องสามเหลี่ยมคล้าย เช่น รูปสามเหลี่ยม ABC คล้ายกับรูปสามเหลี่ยม CEF เมื่อ   

∆ ABC คล้ายกับ  ∆DEFเขียนแทนด้วยสัญลักษณ์ ∆ABC = ∆DEF

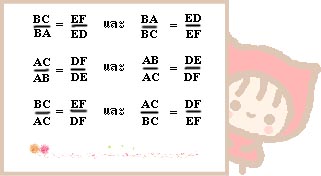
                เมื่อ ∆ABC = ∆DEF จะได้

                             ในการหาความยาวด้านใดด้านหนึ่งของรูปสามเหลี่ยมที่มีขนาดใหญ่มาก อาจใช้การคำนวณเทียบอัตราส่วนกับรูปสามเหลี่ยมคล้ายที่มีขนาดเล็กกว่าได้

1 /2 /3 /4 /5 /6 /7 /8