หลักการแก้ปัญหา  

     ในชีวิตประจำวันทุกคนจะต้องเคยพบกับการแก้ปัญหาต่างๆ ไม่ว่าจะเป็นการแก้ปัญหาทางด้านการเรียน การงาน การเงิน ฯลฯ ซึ่งแต่ละคนก็มีวิธีในการแก้ปัญหาแตกต่างกันไป แต่ถ้านำวิธีการแก้ปัญหาต่างๆ มาศึกษาพิจารณา จะพบว่าสามารถสรุปเป็นทฤษฏีได้ นักวิชาการทางด้านการศึกษาที่ให้ความสนใจศึกษาในเรื่องเหล่านี้ ส่วนใหญ่มักจะสรุปตรงกันว่า การเรียนรู้วิธีการแก้ปัญหาเป็นการเรียนรู้ในระดับสูงที่ต้องอาศัยความสามารถ ความรู้ ประสบการณ์ของผู้เรียนรู้ ก่อนที่จะทราบถึงกระบวนการที่จำเป็นต่อการแก้ปัญหา ลองมาศึกษาแก้ไขปัญหาตามกิจกรรมต่อไปนี้

     ตัวอย่างที่ 1 บุรุษไปรษณีย์จำเป็นต้องเดินทางไปเก็บจดหมายที่ตู้ไปรษณีย์และนำกลับมายังที่ทำการไปรษณีย์สำนักงานใหญ่    ให้หาว่าเส้นทางไหนใช้เวลาในการเดินทางน้อยที่สุด และเดินทางเป็นเวลากี่หน่วย จากรูปที่ 8.1 จำนวนต่างๆ ในรูปแสดงเป็นหน่วยของเวลาที่ใช้ในการเดินทางจากตู้ไปรษณีย์หนึ่งไปยังตู้ไปรษณีย์อีกแห่งหนึ่ง โดยมี A คือจุดเริ่มต้น และ H คือที่ทำการไปรษณีย์สำนักงานใหญ่

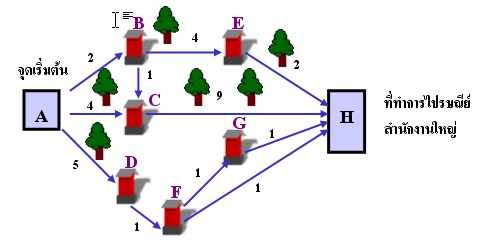
แสดงเส้นทางเชื่อมจากจุดเริ่มต้นผ่านตู้ไปรษณีย์ต่างๆ ไปยังสำนักงานใหญ่

     การแก้ปัญหาในตัวอย่างที่ 1 นี้สามารถทำได้หลายแบบ บางคนอาจจะคาดคะเนโดยพิจารณาจากที่จุดเริ่มต้นว่าเส้นทางที่จะไปที่ตู้ไปรษณีย์ถัดไปเส้นทางไหนที่ใช้เวลาในการเดินทางน้อยที่สุด เมื่อถึงจุดถัดไปก็ทำการเปรียบเทียบหาเส้นทางที่ใช้เวลาน้อยที่สุดไปเรื่อยๆ จนถึงที่ทำการไปรษณีย์สำนักงานใหญ่ ซึ่งวิธีนี้อาจจะไม่ใช่วิธีที่ดีสุด เพราะการแก้ปัญหาควรจะดูเส้นทางทั้งหมด

     การแก้ปัญหานี้ที่ถูกต้องควรหาเวลาที่ใช้ในการเดินทางของแต่ละเส้นทางแล้วพิจารณาว่าเส้นทางไหนใช้เวลาน้อยที่สุด จากปัญหาที่กำหนดเส้นทางทั้งหมดที่สามารถเดินทางได้มี 5 เส้นทางและเวลาที่ใช้ในแต่ละเส้นทางเป็นดังนี้  
 

     1. A -> B -> E -> H = 8
     2. A -> B -> C -> H = 12
     3. A -> C -> H = 13
     4. A -> D -> F -> H = 7
     5. A -> D -> F -> G -> H = 8  
     เส้นทางที่ใช้เวลาในการเดินทางน้อยที่สุดคือเส้นทาง A -> D -> F -> H  ซึ่งใช้เวลาในการเดินทาง 7 หน่วยเวลา

     จากการศึกษาพฤติกรรมของมนุษย์เกี่ยวกับวิธีการเรียนรู้และวิธีการแก้ปัญหา พบว่ากระบวนการที่ทำให้ประสบผลสำเร็จในการแก้ปัญหาควรมีขั้นตอน ดังนี้

     1. การวิเคราะห์และกำหนดรายละเอียดของปัญหา ในการที่จะแก้ปัญหาใดปัญหาหนึ่งได้นั้น สิ่งแรกที่ต้องทำคือทำความเข้าใจเกี่ยวกับถ้อยคำต่างๆ ในปัญหา แล้วแยกปัญหาให้ออกว่าอะไรเป็นสิ่งที่ต้องหา แล้วมีอะไรเป็นข้อมูลที่กำหนด และมีเงื่อนไขใดบ้าง หลังจากนั้นจึงพิจารณาว่าข้อมูลและเงื่อนไขที่กำหนดให้นั้นเพียงพอที่จะหาคำตอบของปัญหาได้หรือไม่ ถ้าไม่เพียงพอ ให้หาข้อมูลเพิ่มเติมเพื่อที่จะสามารถแก้ไขปัญหาได้

     2. การวางแผนในการแก้ปัญหา จากการทำความเข้าใจกับปัญหาจะช่วยให้เกิดการคาดคะเนว่าจะใช้วิธีการใดในการแก้ปัญหาเพื่อให้ได้มาซึ่งคำตอบ ประสบการณ์เดิมของผู้แก้ปัญหาจะมีส่วนช่วยอย่างมาก ฉะนั้นในการเริ่มต้นจึงควรจะเริ่มด้วยการถามตนเองว่า  "เคยแก้ปัญหาในทำนองเดียวกันนี้มาก่อนหรือไม่" ในกรณีที่มีประสบการณ์มาก่อนควรจะใช้ประสบการณ์เป็นแนวทางในการแก้ปัญหา สิ่งที่จะช่วยให้เราเลือกใช้ประสบการณ์เดิมได้ดีขึ้นคือ การมองดูสิ่งที่ต้องการหา และพยายามเลือกปัญหาเดิมที่มีลักษณะคล้ายคลึงกัน เมื่อเลือกได้แล้วก็เท่ากับมีแนวทางว่าจะใช้ความรู้ใดในการหาคำตอบหรือแก้ปัญหา โดยพิจารณาว่าวิธีการแก้ปัญหาเดิมนั้นมีความเหมาะสมกับปัญหาหรือไม่ หรือต้องมีการปรับปรุงเพื่อให้ได้วิธีการแก้ปัญหาที่ดีขึ้น ในกรณีที่ไม่เคยมีประสบการณ์ในการแก้ปัญหาทำนองเดียวกันมาก่อน ควรเริ่มจากการมองดูสิ่งที่ต้องการหา แล้วพยายามหาวิธีการเพื่อให้ได้ความสัมพันธ์ระหว่างสิ่งที่ต้องการหากับข้อมูลที่มีอยู่ เมื่อได้ความสัมพันธ์แล้วต้องพิจารณาว่าความสัมพันธ์นั้นสามารถหาคำตอบได้หรือไม่ ถ้าไม่ได้ก็แสดงว่าต้องหาข้อมูลเพิ่มเติมหรืออาจจะต้องหาความสัมพันธ์ในรูปแบบอื่นต่อไป เมื่อได้แนวทางในการแก้ปัญหาแล้วจึงวางแผนในการแก้ปัญหาเป็นขั้นตอน 

     3. การดำเนินการแก้ปัญหาตามแนวทางที่วางไว้ เมื่อได้วางแผนแล้วก็ดำเนินการแก้ปัญหา ระหว่างการดำเนินการแก้ปัญหาอาจทำให้เห็นแนวทางที่ดีกว่าวิธีที่คิดไว้ ก็สามารถนำมาปรับเปลี่ยนได้

     4. การตรวจสอบ เมื่อได้วิธีการแก้ปัญหาแล้วจำเป็นต้องตรวจสอบว่า วิธีการแก้ปัญหาได้ผลลัพธ์ถูกต้องหรือไม่

     ตัวอย่างต่อไปนี้จะพิจารณาการแก้ปัญหาตามแนวทางของการแก้ปัญหาดังที่ได้กล่าวไว้ แต่จะเน้นที่ขั้นตอนการวิเคราะห์และกำหนดรายละเอียดของปัญหา และการวางแผนซึ่งเป็นขั้นตอนที่สำคัญ

     ตัวอย่างที่ 2 ให้เติมตัวเลข 1-6 ลงในวงกลมที่จัดวาง ดังรูปที่ด้านล่าง โดยตัวเลขในวงกลมจะต้องไม่ซ้ำกัน และผลรวมของตัวเลขในวงกลมที่เรียงกันแต่ละด้านมีค่าเท่ากัน  

แผนภาพสำหรับวางตัวเลข 1-6

     ขั้นตอนที่ 1 วิเคราะห์และกำหนดรายละเอียดของปัญหา
     จากปัญหาข้างต้น พบว่า สิ่งที่ต้องการให้หา คือ การใส่ตัวเลข 1-6 ลงในวงกลม ที่อยู่ในตำแหน่งที่กำหนดดังรูปด้านบน  เพื่อให้ได้ผลบวกของตัวเลขสามตัวที่อยู่ในวงกลมที่เรียงในแต่ละด้านมีค่าเท่ากัน
     ข้อมูลที่กำหนดให้ คือ ตัวเลข 1-6 และรูปแบบการเรียงกันของวงกลมที่จะบรรจุตัวเลขดังรูป 

     สิ่งที่จะต้องพิจารณาต่อไปคือพิจารณาความเป็นไปได้ในการแก้ไขว่าเป็นไปได้หรือไม่ หรือกล่าวให้แคบลงคือพิจารณาว่าจากข้อมูลและเงื่อนไขที่กำหนดให้นั้นเพียงพอที่จะหาคำตอบของปัญหาได้หรือไม่ ในตัวอย่างข้างต้นจะเห็นได้ชัดว่าเมื่อกำหนด ตัวเลข 1-6 และ รูปแบบสามเหลี่ยมที่มีวงกลม 6 วง แต่โจทย์ไม่ได้กำหนดผลรวมว่าเป็นเท่าใด ดังนั้นจึงต้องมีการพิจารณาว่าผลรวมที่เป็นไปได้มีทั้งหมดกี่วิธี แต่ละวิธีจะมีรูปแบบการวางตัวเลขที่แตกต่างกันหรือไม่  
 
     ขั้นตอนที่ 2 วางแผนในการแก้ปัญหา
     เมื่อทำความเข้าใจกับปัญหาแล้ว จะเห็นว่าสิ่งที่จะต้องพิจารณาในการวางแผนเป็นสิ่งแรกคือการหาผลบวกของจำนวนในแต่ละด้านว่าควรเป็นเท่าไรและหาได้อย่างไร ในที่นี้จะพิจารณาผลบวกที่มีค่าน้อยที่สุดและผลบวกที่มีค่ามากที่สุด ซึ่งจะทำให้ทราบว่าผลบวกจะอยู่ในช่วงใด

     เนื่องจากรูปแบบวงกลมที่จะใส่ตัวเลขลงไปวางเรียงกันอยู่ในแนวด้านสามด้านของรูปสามเหลี่ยม และจะเห็นว่าตัวเลขที่ใส่อยู่ในวงกลมตรงจุดมุมจะได้รับการนำไปบวกในสองด้าน ทำให้มีการนำไปบวกซ้ำในการหาผลบวกของทั้งสามด้าน

     ดังนั้น สูตรในการหาผลบวกที่มีค่าน้อยที่สุด คือ
     (ผลบวกของจำนวนทั้ง 6 จำนวน + ผลบวกน้อยที่สุดของจำนวนที่มีการบวกซ้ำ) /3 
     และสูตรในการหาผลบวกที่มีค่ามากที่สุด คือ  
     (ผลบวกของจำนวนทั้ง 6 จำนวน + ผลบวกมากที่สุดของจำนวนที่มีการบวกซ้ำ) /3 

     จะได้ผลบวกที่มีค่าน้อยที่สุด คือ  (21+6) / 3 = 9  
     เพราะผลบวกของจำนวนทั้ง 6 จำนวน คือ 1+2+3+4+5+6 = 21  
     และผลบวกน้อยที่สุดของจำนวนที่มีการบวกซ้ำ คือ  1+2+3 = 6  
 
  
 

     ผลบวกที่มีค่ามากที่สุด คือ  (21 + 15) / 3 = 12  
     เพราะผลบวกทั้งหมด คือ 1+2+3+4+5+6 = 21  
     และผลบวกมากที่สุดของจำนวนที่มีการบวกซ้ำ คือ 6+5+4 = 15 
 
 

     ดังนั้นผลบวกด้านแต่ละด้านของรูปสามเหลี่ยม จะอยู่ในช่วง 9-12

     ขั้นตอนที่ 3 ดำเนินการตามแผนที่วางไว้
     ขั้นตอนต่อไปคือการพิจารณาวางตัวเลขทั้งหกลงในวงกลมเพื่อให้ได้ผลบวกเป็น 9, 10 ,11 และ 12 และการวางตัวเลขเพื่อให้ได้ผลบวกดังกล่าวอาจเป็นดังต่อไปนี้ 

    

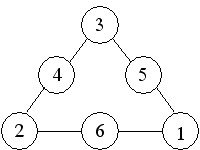
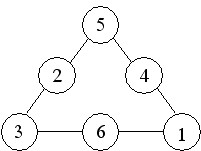
                                             ผลบวก =9                                         ผลบวก =10

    
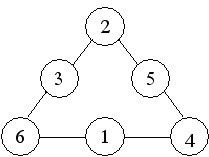
  ผลบวก =11                                       ผลบวก =12
 

     ขั้นตอนที่ 4 ตรวจสอบความถูกต้อง